Collision Detection – Circles, Rectangles and Polygons

Sharing is caring!

Collision Detection – Circles, Rectangles and Polygons

So you’re making a game and you want to check if your character has bonked an enemy. This calls for collision detection algorithms. Surely you could use a framework like Box2D to do all the collision detection for you.. well yes,  you could and it would work pretty darn good. But if you don’t really need all the physics processing that comes with Box2D then you’re adding a lot of bloat to your game when it could be done with some nice algorithms shown in this guide.

Circle vs Circle

So how do we detect of 2 circles are colliding? Well, lets take a look at 2 circles colliding and see what we can tell:

If you look at this image you can see the radius of circle 1 (the red line) and the radius of circle2 (the blue line) when both circle touch create a line between the centers of both circles. Any further apart and they would not be touching and any closer and they would be inside each other. This works for any angle too.

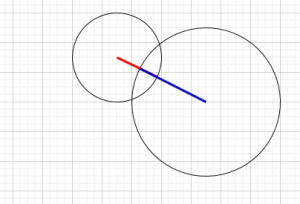So now we know if the distance between the circles is smaller than the combined radius of both circles then the circles are colliding. So how do we work out the distance between the 2 circles?  If we draw a line on the x axis from 1 circle to the other  and one on the y axis we get this:

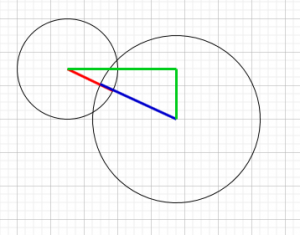Oh look, a triangle…. and not just any triangle, a right angled triangle.  Now we have a right angled triangle we can use Pythagorean theorem to work out the distance. The Pythagorean theorem states that the hypotenuse (the side opposite the right angle) is always the square root of side 1 squared + side 2 squared. For us to get the x axis length values we would take the absolute value(non negative) of circle 1’s x position – circle 2’s x position this gives us one side of the triangle. Now we do the same on the y axis using circle’s y  position – circle2’s y position. The code for this is:

Now we square the side values

Now we get the square root

We now have the distance between the 2 circles. The last thing is to compare it to the sum of the circle’s radii..(radiuses?!?)

To make this more useful we can put it all in one method so all we have to do is ask is circle1 touching circle 2 and that is done with this method.

Rectangle vs Rectangle

A rectangle in computing usually refers to a shape with 4 corners and 2 parallel sides and is a common shape for use in collision detection due to its simplicity to make and detect collisions with. Rectangles are often used to define a collision boxes for entities that don’t require precise detection. So how do we check if 2 rectangles are colliding? we check to see if 2 of the sides fall in between the other rectangle. Lets take a look at two rectangles about to collide:

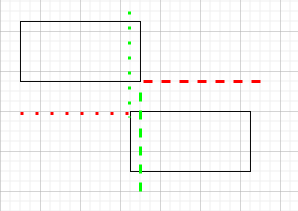
Here you can see 2 rectangles that have not collided yet. You can see by the dotted lines that neither the bottom nor right edge fall inside the other rectangle. This says the rectangle is not colliding.

Now you can see that one side of each rectangle is inside the other and this means.. well, it means nothing they still haven’t collided only one side of each is inside and for a collision 2 sides must be inside the other rectangle.

A collision has happened and both sides of each rectangle are inside the other rectangle. O.k. so now we know how to check if a rectangle is in a rectangle but how do we do this in code?

First, we must find out where the sides of the rectangle are and we do that using the width, height and position of the rectangle. In our example we will be using the position as the bottom left corner but you could use the center of the rectangle with a little extra math. So first we need to get the position of all sides:

We do the same for rectangle 2 and then we compare using the following code:

Now we can tell when 2 sides are inside another rectangle we just need to combine them in a single function we can call whenever we need to:

Simple Polygon vs Polygon (convex)

So we covered circles and rectangles but how about polygons. Polygons don’t have a set radius or a set width and height so we can’t use the previous methods. Let’s take a look at some polygons that are colliding and see what we can tell about polygon collisions.

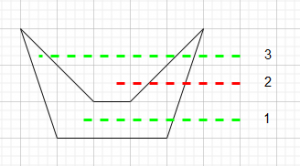
From this image you can see that if a convex polygon is colliding then at least 1 of the corners(vertices) is inside the other polygon. So if we check to see if a corner point is inside the other polygon we know they are colliding There are some edge cases where the points do not fall within the other polygon however this is not covered in this guide as it is only an introduction to collision detection. So how do we check if a point is inside a polygon? We simply draw a line from the point to somewhere external to the polygon.

In the image above you can see we have drawn 3 dashed lines. 2 of the lines start inside the concave polygon and those have cross the polygon border an odd amount of times whereas the line that starts outside the polygon crosses the border an even number of times. By checking if a line we draw from the point crosses the polygon border an odd amount of times we will be able to tell if a point is inside a convex or concave polygon. Note: We will only checking for convex polygons with our code however, I just wanted to show that this line method works for both types when checking points.

Breaking up the polygon

In order to start drawing imaginary lines through our polygon, we need to first break the polygon up into segments. Each segment will be a pair of corners  which will be one border of the polygon like the green line in the image below:

We first need to iterate through all the vertices. In this tutorial our polygon vertices are stored as an array of floats. In the image above the red arrow shows the order the vertices are stored. So our array of vertices for this pentagon shape would be {1,0,0,3,3,6,6,3,5,0}  which equates to  {x1,y1,x2,y2,x3,y3,x4,y4,x5,y5}. So to loop over these values we will use this for loop:

Now we have a loop we can work out the formulas.

From the image above you can see that our first vertex is x1 and y1 and then the next vertex is x2 and y2. This is due to the order the vertexes are inside the float array. Now we have the vertex values we need to get the gradient ( the slant of the line between the two vertex points ). With the gradient we can find out the length of d by multiplying the gradient by the distance down the line to the point. This gives us the x position of Px.

Now we have the x position of Px we can see if the point we are checking is directly left of this border line. If Px is left of this line then we can say we have found 1 of the points where our imaginary line crosses a border and can increment an intersect counter.

So how do we put all this into a function?

We have a function to check if a point is in a polygon and it can be used for every vertex in a polygon to allow us to check if a polygon is in a polygon. So if all 5 points of a pentagon are not inside a polygon then we know the polygons are not colliding and if at least one point is inside then we know the polygon is colliding. The code for that is:

Why can’t we use this method to check concave polygons?

Concave polygons can have parts that extrude out and allow vertices to completely go through another polygon and this stops our function from returning true as we’re only checking if points are inside a polygon. If you need to check convex polygons I recommend using the separating axis theorem method.

Shape A vs shape B

Checking for one shape versus another is a little more complex than what we’ve been doing before. First you need to be able to know what shapes are colliding then use an appropriate algorithm. This however is outside the scope of this tutorial and we will only be going over how to check for collisions between set shapes. We will go over Circle vs Polygon, Circle vs Rectangle and  Rectangle vs Polygon.

Rectangle vs Polygon

We have already covered how to check if a polygon is inside another polygon and we broke it into parts and checking each corner of the polygon as a point. A Rectangle is just a polygon with 4 corners. We can reuse the code we made for the polygon vs polygon code. We just need to get the rectangle corners from the height, width and position of the rectangle. An that is done with this code:

Now you can iterate over them like you did with the polygon’s vertices.

Circle vs Polygon

This is where things get complicated. An explanation as simply as possible is…. you take a single border of a polygon, get its width and height and turn it into a vector (value stating direction). Next, you get a vector to represent a line to the centre of the circle. Normalize this value and find the dot product between this line and the first line. This will give us 0 or less when the circle is closest to the start of the line , line length or more when closest to the end of the line and a value between 0 and line length when closest to a middle part of our polygon border line. Now we get the x and y position closest to the circle centre, square them and compare vs the square of the circle radius. If the radius squared is less than the squared x y position of the closest point it is colliding.

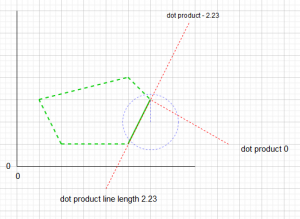
That’s quite a lot to take in so we’ll break it down into smaller portions. The first thing we are doing is finding the vector of the line between the two points of the polygon. Shown in the image below:

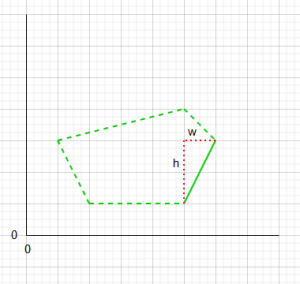In the image, the solid green line is the vector we are checking. We get the width of the line by removing the x value for the first point from the x value of the second point( the top point is first due to the ordering of the vertices in the float array for the polygon) This gives us negative 1. Next we get the y value be removing the y value of the start point from the end point. This gives us negative 2, so our border line is now represented as a vector of (-1,-2).

Now we need to get the vector for the circles center from the start point. This is done by removing the circle x from the start x and the circle y from the start y. In the image you can see the dotted red line which represents our new vector and  and equates to (0,-1). Now we have 2 vectors which we will use to get the length and the dot product. The length we will store for later and can be worked out manually by getting the square root of w*w + h*h. The dot product is a measurement of the similarity of 2 vectors. If 2 vectors are pointing in the same direction the dot product will be 1, if the two vectors are opposite then the dot product will be -1 and a right angle would be 0. This is true in maths however in programming the dot product will not range from -1 to +1 instead it will range from -line length to +line length but 0 will always represent a 90 degree angle.

First we get the length of the line in the image above:

Now the dot product:

If we look at the image above we can see that if the dot product is below 0 the circle center would be in the top right quarter. If the dot product is bigger than the line length then the circle would be in the lower left quarter. Now we have the dot product and it is less than the line length of 2.2 but more than 0. Now we know the center of the circle is in the lower right quarter and is closest to a point on our polygon border.

Now we need to find out which point that is. We already have all the variables we need from the previous calculations; the dot product and the normalized borderVector. To get this point we just need to scale the borderVectorNormal by the dot product and add those to the start.x and start.y

The output vector now contains the x and y position on the polygon border that our circle center is closest to.

The final calculation checks if the circle is close enough to be considered colliding using the euclidean distance:

As you can see from the formula and image above we use the x and y value to create a triangle and then work out the hypotenuse length. Then we check if the hypotenuse is smaller than the radius to check if the circle is colliding.

So now we can check if a circle is colliding with a single border line from our polygon but only when the circle is closest to the border line. we haven’t done any checks for when the circle is closest to the start or end point of our line. This function below does contain those cases and can be used to check if a circle intersects a polygon border line:

We now need to check each line in our polygon to check collisions for all sides. We can reuse our loop we used for checking polygon vs polygon collisions. So our finished code looks like this:

Circle vs Rectangle

Checking a rectangle against a circle is the same as checking a polygon against a circle we just need to convert the corners to vertices like we did for the Rectangle vs polygon answer.

This however is quite expensive and another method is available if the rectangles are never rotated and always align with the x and y axis shown in the next section.

Circle vs Rectangle (Axis Aligned)

To check if an axis aligned rectangle is colliding with circle you can inflate the rectangle with the radius of the circle and then check if the circle center lies within this area.

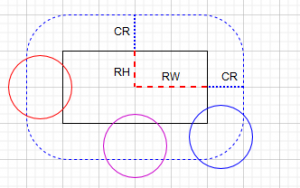
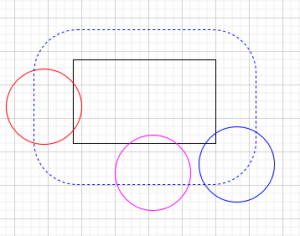In the image above you can see 3 circles all colliding with a rectangle from the sides and on the corner. All of them have their center within our inflated rectangle. So how do we create this in code?

The first thing we need to do is get the distance the circle is from the rectangle for each axis.

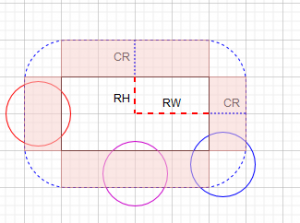
If you look at the image above you can see that the rectangle width(RW) plus the circle radius(CR) gives us our outer bounds for the circle collision anything that is bigger than this is not going to be colliding and can be excluded from any further calculations. (All of our circles pass this test)

Now we check if the circle center is inside rectangle or the red areas of the image above using the following code:

The red and purple circle have been detected by this and are considered to be colliding, the blue isn’t inside these and will be caught by the next check.

Now we have to check the corners to check if the circle centers lie with in them. In order to do that we have to get the euclidean distance from the center of the circle to the center of the rectangle.

finally we check if the radius squared is smaller or equal to the euclidean distance. This captures our final circle  and concludes all the phases of checking collisions.

So our final code for checking collisions between Circles and axis aligned rectangles is:

Notes.. and why I use Libgdx.

I prefer to use a framework such as Libgdx to create my games and thought it would be good to show you how all these collision detections would be done when using the Libdx framework. Nearly all  of the collision detection methods shown above can be done in libgdx using the Intersector class.

Circle vs circle

Rectangle vs Rectangle

Polygon vs Polygon

Rectangle vs polygon

Circle vs polygon

Circle vs rectangle

As you can see the amount of coding needed is considerably less when using Libgdx.

 

 

 

 

Sharing is caring!